Развертка пирамиды. Контрольная по начертательной геометрии под редакцией П.В. На Студопедии вы можете прочитать про: Сечение плоскостью призмы, пирамиды, цилиндра. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ Тема 0. Поэтому построение развертки пирамиды сводится. Подробно рассмотрен способ построения развертки пирамиды. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ.

• Инженерная Графика
• Развертка Треугольной Пирамиды Начертательная Геометрия
• Метод Монжа
• Начертательная Геометрия 1 Курс

Развёртка поверхности это фигура, получающаяся в плоскости при таком совмещении точек данной поверхности с этой плоскостью, при котором длины линий остаются неизменными. При этом каждой точке поверхности соответствует единственная точка на развёртке.

Примеры построения линий перехода и положения темы: 1). При изготовлении различных изделий из листового материала имеет большое значение построение разверток поверхностей.

Если представить себе поверхность как гибкую нерастяжимую пленку, то некоторые из них путем изгиба можно совместить с плоскостью без разрывов и деформаций. Такие поверхности относятся к развертываемым. Полученную в результате развертывания (раскатки) поверхности плоскую фигуру называют разверткой этой фигуры. Те поверхности, которые нельзя совместить без разрывов и деформаций, относятся к неразвертываемым, но в практике возникает необходимость изготовления из листового железа не только развертывающихся фигур. Теоретически точно развертываются только гранные поверхности, торсы, конические или цилиндрические поверхности. При развертывании сложных поверхностей их аппроксимируют (заменяют) вписанными гранными поверхностями, и чем больше граней содержит вписанная поверхность, тем точнее ее развертка.

Построенные таким образом развертки поверхностей называют приближенными. Чтобы построить развертки неразвертывающихся поверхностей, эти поверхности разбивают на части, которые можно приближенно заменить развертывающимися поверхностями. После этого строят развертки этих частей, которые в сумме дают условную развертку неразвертывающейся поверхности. Разверткой поверхности многогранника называют плоскую фигуру, полученную при совмещении с плоскостью чертежа всех граней многогранника в последовательности их расположения на многограннике. Чтобы построить развертку поверхности многогранника, нужно определить натуральную величину граней и вычертить на плоскости последовательно все грани.

Истинные размеры ребер граней, если они спроецированы не в натуральную величину, находят способами вращения или перемены плоскостей проекций. Развертка поверхности прямой призмы представляет собой плоскую фигуру, составленную из боковых граней прямоугольников и двух равных между собой многоугольников оснований.

Для примера взята правильная прямая шестигранная призма (рис. Все боковые грани призмы прямоугольники, равные между собой по ширине а и высоте Н; основания призмы правильные шестиугольники со стороной, равной. Так как истинные размеры граней нам известны, нетрудно выполнить построение развертки. Для этого на произвольной горизонтальной прямой последовательно откладываем шесть отрезков, равных стороне основания шестиугольника, т. Из полученных точек проводим перпендикуляры, равные высоте призмы Н, и конечные точки перпендикуляров соединяют второй горизонтальной прямой. Полученный прямоугольник (Н х 6а) Рисунок 56 Развертка шестигранной призмы является разверткой боковой поверхности призмы.

Затем пристраиваем фигуры оснований два шестиугольника со сторонами, равными. Контур обводят сплошной основной линией, а линии сгиба штрихпунктирной с двумя точками.

Подобным образом можно построить развертки прямых призм с любым многоугольником в основании. На рисунке 57 изображена развертка трехгранной призмы правильной формы. Ребра ее АА, ВВ, СС параллельны фронтальной плоскости П2 проекций и проецируются на нее в натуральную величину, а нижнее ABC и верхнее А’В’С’ основания параллельны горизонтальной плоскости проекций П1 и проецируются на нее в натуральную величину. Точка М на развертке трехгранной призмы строится обычным способом. Рисунок 57 Развертка трехгранной призмы 5).

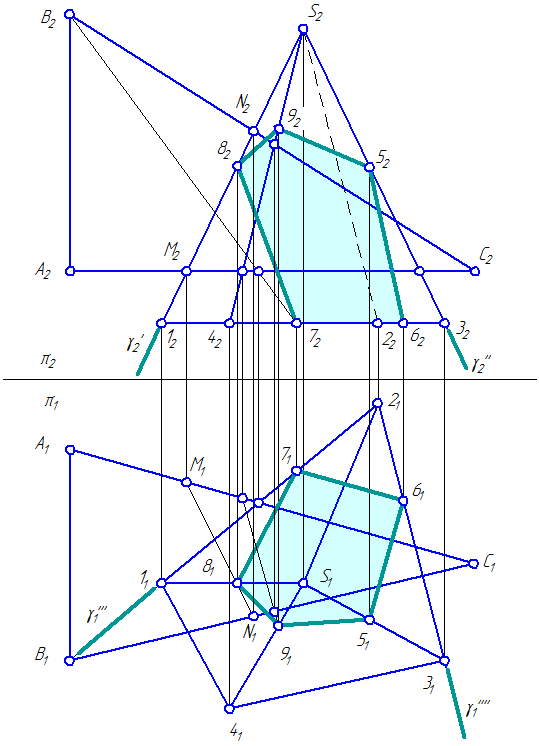
Развертка поверхности правильной пирамиды представляет собой плоскую фигуру, составленную из боковых граней равнобедренных или равносторонних треугольников и правильного многоугольника основания. Для примера взята правильная четырехугольная (четырехгранная) пирамида (рис. Решение задачи осложняется тем, что неизвестна величина боковых граней пирамиды, так как ребра граней не параллельны ни одной из плоскостей проекций. Поэтому построение начинаем с определения истинной величины наклонного ребра SA. Определив способом вращения истинную длину наклонного ребра SA, равную s’а1′, из произвольной точки О, как из центра, проводим дугу радиусом s’а1′. На дуге откладывают четыре отрезка, равные стороне основания пирамиды, которое спроецировано на чертеже в истинную величину. Полученные точки соединяем прямыми с точкой О.

Получив развертку боковой поверхности, к основанию одного из треугольников пристраиваем квадрат, равный основанию пирамиды. Рисунок 58 Развертка четырехугольной пирамиды 6). На рисунке 59 приведен еще один вариант построения развертки четырехгранной прямой пирамиды. Построение ее упрощается тем, что образующие пирамиды AS и CS параллельны фронтальной плоскости проекций и на нее спроецировались в натуральную величину. Основание же пирамиды ABCD лежит в плоскости, параллельной горизонтальной плоскости проекций, и на нее проецируется в натуральную величину. Для построения развертки достаточно построить сторону AS и сделать засечки радиусом дуги, равным BS и АВ из точек S и А, соответственно получим точку В и т. Основание же в натуральную величину можно построить на базе одной из его сторон, например, на базе стороны АВ.

Положение точки на поверхности развертки пирамиды определим в следующем порядке: через фронтальную проекцию точки М (М2) проведем горизонтальную линию до пересечения с ребрами A2S2 и B2S2. Получим фронтальные проекции точек 1 и 2, далее определим их горизонтальные проекции. На линии AS развертки от точки А отложим отрезок h и из полученной точки 1 проведем линию 1, 2 параллельно AD на которой нанесем точку М в том положении, которое она занимает на горизонтальной проекции линии 12. Рисунок 59 Нахождение точки на развертке 7). Развертка поверхности прямого кругового конуса представляет собой плоскую фигуру, состоящую из кругового сектора и круга (рис. Чтобы ее построить, проводим осевую линию и из точки, взятой на ней, как из центра, радиусом равным образующей конуса, очерчивают дугу окружности.

В данном примере образующая, подсчитанная по теореме Пифагора, равна приблизительно 38 мм (L = √l52 + 352 = √l450 ≈ 38 мм). Рисунок 60 Развертка прямого конуса Затем подсчитываем угол сектора по формуле: где R радиус окружности основания конуса; L длина образующей боковой поверхности конуса. В данном примере α = 360° х 15/38 ≈ 142,2°. Этот угол строят симметрично относительно осевой линии с вершиной в точке S. К полученному сектору пристраиваем круг с центром на осевой линии и диаметром, равным диаметру основания конуса.

На рисунке 61 приведен еще один вариант построения развертки прямого кругового конуса. Для построения ее используем то, что очерковая образующая конуса на фронтальной плоскости изобразилась в натуральную величину. Выбрав положение вершины развертки точку S, радиусом, равным величине образующей, проводим дугу и откладываем на ней 12 равных частей, на которые предварительно разделили окружность основания конуса, изображенного на горизонтальной плоскости проекции в натуральную величину. Чем на большее количество равных участков разделим окружность, тем точнее построим развертку. Положение точки М на развертке поверхности конуса определим следующим образом: через фронтальную проекцию точки проведем образующую и построим горизонтальную ее проекцию.

Найдем, что образующая пересекла основание конуса между точками 5 и 6. Точку К переносим на дугу развертки, расположив ее между точками 5 и 6, и соединим с вершиной конуса развертки S.

Из проекции точки M2 проведем горизонтальную линию до пересечения с очерковой образующей и получим новое положение фронтальной проекции точки М. Расстояние от основания конуса до этой проекции по образующей является высотой точки h, которую откладываем на развертке от точки К на линии KS это истинное положение точки M на развертке. Таким образом, развертку конической поверхности построим с помощью соседних точек окружности основания, в которую мысленно вписан правильный двенадцатиугольник. Коническая поверхность условно заменена поверхностью, а именно, правильной двенадцатиугольной пирамидой, а для построения развертки применен способ триангуляции. Рисунок 61 Нахождение точки на развертке конуса 9). Построение развертки прямого кругового цилиндра приведено на рисунке 62. Высота цилиндра Н, на фронтальную плоскость проекций П2 она проецируется в натуральную величину.

Нижнее и верхнее основания параллельны горизонтальной плоскости проекций П1 и на нее проецируются в натуральную величину. Рисунок 62 Развертка цилиндра В этом случае развертку цилиндрической поверхности строим с помощью хорд, соединяющих соседние точки деления окружности оснований, в который вписан правильный двенадцатиугольник. В этом случае цилиндрическая поверхность условно заменена поверхностью вписанной правильной двенадцатигранной призмы, и развертка цилиндрической поверхности построена способом триангуляции. Шар (сфера) относится к геометрическим телам, поверхности которых не могут быть точно развернуты на плоскости без складок и разрывов.

Приближенные развертки шара строят различными способами. Способ веретен основан на том, что поверхность шара заменяют поверхностью большого количества полос, суживающихся к полюсам и имеющих наибольшую ширину на экваторе (рис. На чертеже поверхность шара разделена на 12 равных частей, одна из которых изображена. Как видно, она расположена симметрично относительно фронтального меридиана. Делим фронтальную проекцию полосы на равные части и определяем длину образующих в точках деления. Очевидно, что длина образующих проецируется без искажения на плоскость П1. Развертываем цилиндрическую полосу (рис.

63б), беря вертикальные размеры с фронтальной проекции шара, а горизонтальные 2030, 4050 и 6070 с горизонтальной проекции шара. Аналогично строим нижнюю часть развертки. Полученные точки соединяем плавной кривой. Развертка шара по форме напоминает веретено. Рисунок 63 Способ веретен 3.11. Задание на выполнение эпюра 4 Эпюр 4: 1). Построение линии пересечения заданных поверхностей.

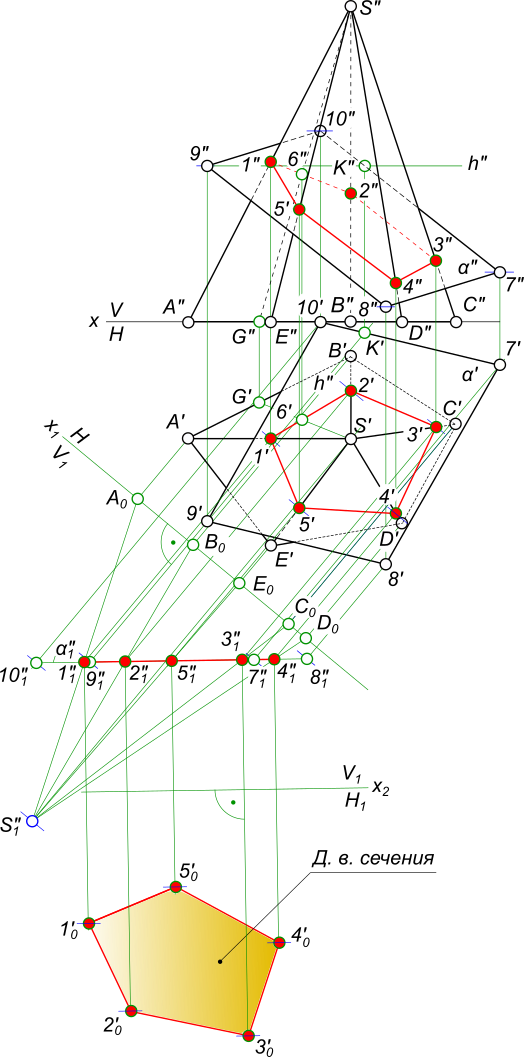
Выполнение развертки одной из поверхностей с обязательным нанесением линии пересечения. Варианты заданий размещены на страницах 72 и 73. Пример выполнения задания приведен на рисунке 64. Рекомендации к выполнению эпюра 4 Секущие плоскости для нахождения линии пересечения необходимо выбирать так, чтобы обе поверхности пересекались по наиболее простым линиям окружностям или образующим. На чертеже должны быть сохранены все линии построения, следы вспомогательных плоскостей, обозначены все точки. Проекции линии пересечения лучше обвести линиями красного цвета с учетом видимости.

Разверткой конуса вращения является круговой сектор с углом ϕ = R ⋅ 3600, где R радиус основания конуса, l длина образующей. На l развертке строят прямолинейные образующие или параллели, проходящие через характерные точки линии пересечения. Построенные точки соединяют плавной линией красным цветом. При построении развертки цилиндра проводят горизонтальную линию длиной 2πR, где R радиус основания цилиндра. Строят развертку боковой поверхности, где отмечают прямолинейные образующие, проходящие через характерные точки линии пересечения, которые соединяют плавной кривой линией.

Для полной развертки в обоих случаях к боковой поверхности пристраивают основание. Формат чертежа A3.

Масштаб эпюра 1:1. Вопросы для самопроверки усвоения учебного материала К эпюру 1: 1. Повторите наименования плоскостей проекций, координатных осей, линий связи. Покажите построение точек в трёх проекциях. Какие точки называют точками общего, а какие частного положения?

Каким образом можно задать прямую линию на чертеже? Укажите частные положения отрезков прямых линий. Какие прямые называют линиями уровня, проецирующими прямыми?

Инженерная Графика

Как выглядит проекция прямого угла в общем случае? При каких условиях прямой угол проецируется в натуральную величину? Перечислите и покажите способы задания плоскости на эпюре. Дайте определение плоскостям общего и частного положения. Поясните особенности проецирующих плоскостей. Как определяется принадлежность прямой линии и точки данной плоскости?

Покажите способы построения проекций горизонтали и фронтали на плоскости общего положения. Какое положение могут занимать прямая линия и плоскость или две плоскости относительно друг друга? Какое условие определяет взаимную перпендикулярность двух плоскостей? Укажите последовательность построения линии пересечения двух плоскостей общего положения. Чем отличается определение линии пересечения плоскостей, если одна из них проецирующая? Как определяют видимость элементов геометрических объектов?

К эпюру 2: 19. Как на чертеже определить истинное расстояние от точки до прямой линии? Каким образом можно на эпюре определить действительное расстояние от точки до проецирующей плоскости или до плоскости общего положения?

В чём заключается принцип преобразования чертежа способом замены плоскостей проекций? Что определяет положение новой плоскости проекций при планируемых преобразованиях эпюра? Какова последовательность решения задач по определению натуральных величин геометрических объектов, углов их наклона и расстояний при использовании способа замены плоскостей проекций? В чем сущность метрических задач? К эпюру 3: 25. Какое определение даётся поверхности?

Каким образом можно задать поверхность на эпюре? Назовите многогранники и иx определители.

Развертка Треугольной Пирамиды Начертательная Геометрия

Перечислите кривые поверхности и способы их задания на чертеже. Укажите основные свойства поверхностей вращения.

Каким образом можно убедиться в принадлежности точки или линии изображенной на эпюре поверхности? Сформулируйте общий алгоритм определения точек линии пересечения поверхности плоскостью. Какие точки линии пересечения поверхности плоскостью называют характерными (главными, опорными)? Изложите сущность способов построения линии пересечения многогранника плоскостью, поверхности вращения плоскостью. Укажите условия, при которых в сечении конуса вращения плоскостью получается окружность, эллипс, гипербола, парабола, пересекающиеся прямые. Сформулируйте алгоритм определения точек пересечения прямой линии с поверхностью.

Перечислите последовательность графических построений при определении точек пересечения прямой линии с многогранными и кривыми поверхностями. Как определить натуральную величину сечений поверхности плоскостью? К эпюру 4: 37. Что называется разверткой геометрического тела? Какие развертки знаете?

Как построить развертку прямого кругового цилиндра и конуса? Что называется линией пересечения двух поверхностей? Основной способ построения линии пересечения поверхностей. Особые случаи пересечения поверхностей. Какие выбираются вспомогательные секущие плоскости для многогранников и сфер?

Алгоритм построения линии пересечения поверхностей. Как определяется видимость линии пересечения и поверхностей на плоскостях проекций? Что представляет собой линия пересечения многогранников в общем случае? Какие точки линии пересечения двух поверхностей называют характерными? Что такое точка перехода видимости?

Метод Монжа

Примечание: Желательно прилагать «черновики» к контрольной работе. Принятые графические обозначения и символы Точки обозначаются прописными буквами латинского алфавита: А, В, С, D, Вспомогательные точки обозначают арабскими цифрами: 1, 2, 3 Линии (прямые и кривые) строчные буквы латинского алфавита: a, b, c, d, Прямые, имеющие специальные обозначения: горизонталь — H, фронталь F. Углы в пространстве строчные буквы греческого алфавита: α, β, γ, Плоскости и поверхности в пространстве прописные буквы греческого алфавита: ∆, Σ, Ψ, Плоскости проекций: горизонтальная плоскость проекций П1 (π1), фронтальная плоскость проекций П2 (π2), профильная плоскость проекций П3 (π3). Дополнительные плоскости проекций: П4 (π4), П5 (π5), П6 (π6) Проекции точек, прямых и плоскостей: на П1 A1, d1, Ψ1, на П2 A2, d2, Ψ2. Следы плоскости: горизонтальный след плоскости Σ Σ1, фронтальный след плоскости Σ Σ2.

Способ задания геометрической фигуры: m (АВ) прямая m задана ее точками А и В (отрезком), Ω (c ∩ d) плоскость Ω задана пересекающимися прямыми c и d, Σ (Σ1, Σ2) плоскость Σ задана своими следами. Символы: параллельность; ⊥ перпендикулярность; ∩ пересечение; ∆ треугольник; прямой угол. Словарь графических терминов Геометрическая фигура любое множество точек. К фигурам относится точка (множество, состоящее из одного элемента), прямая либо кривая линия, плоскость, поверхность, тело. Горизонталь (горизонтальная прямая уровня) параллельна плоскости П1. Гранная поверхность образуется перемещением прямолинейной образующей l по ломаной направляющей m. Конкурирующие точки точки, проекционно-совпадающие на одной из плоскостей проекций.

Горизонтально-конкурирующие точки имеют совпадающие проекции на горизонтальной плоскости проекций; фронтально-конкурирующие точки имеют совпадающие проекции на фронтальной плоскости проекций. Линия проекционной связи (линия связи) линия, перпендикулярная к оси проекций.

На линии связи расположена пара проекций точки. Меридианы это линии, которые получаются при сечении поверхности плоскостями, включающими ось. Меридиан, параллельный фронтальной плоскости проекций, называется главным. Многогранник замкнутая гранная поверхность, имеющая не менее 4-х граней (пирамида, призма, тетраэдр и т.д.). Направляющая поверхности m определяет закон перемещения образующей l.

Образующая поверхности линия l, перемещающаяся в пространстве при образовании поверхности. Опорные точки это крайние точки (верхняя, нижняя, левая, правая, дальняя, ближняя) и точки перехода видимости. Определитель это совокупность геометрических элементов и условий, необходимых и достаточных для однозначного задания поверхности в пространстве и на чертеже. Ортогональное (прямоугольное) проецирование проецирование параллельными лучами из бесконечности под прямым углом к плоскости проекций.

Ось проекций линия пересечения плоскостей проекций. Ось Х12 разделяет плоскости П1 и П2, ось Y13 разделяет плоскости П1 и П3, ось Z23 разделяет плоскости П2 и П3. Иногда ось проекций на чертеже не проводят, но ее расположение всегда известно. Так, ось Х12 всегда горизонтальна.

Очерковая линия это проекция контура на плоскости проекций. Параллель это окружность, по которой перемещаются точки образующей в процессе ее вращения. Плоскость общего положения плоскость, не параллельная и не перпендикулярная ни одной из плоскостей проекций. Плоскость уровня плоскость, параллельная одной из плоскостей проекций. Такие плоскости являются дважды проецирующими, так как на двух плоскостях проекций имеют вид прямой, расположенной под прямым углом к линиям связи.

Поверхность вращения образуется вращением образующей l вокруг оси вращения i. Проецирующая прямая прямая, перпендикулярная одной из плоскостей проекций. Например, фронтально-проецирующая прямая перпендикулярна фронтальной плоскости проекций П2. На эту плоскость прямая cпроецируется в виде точки.

Проецирующая плоскость плоскость, перпендикулярная одной из плоскостей проекций. На комплексном чертеже имеет проекцию, вырожденную в прямую линию именно на той плоскости проекций, которой данная плоскость перпендикулярна.

Так, горизонтально-проецирующая плоскость имеет проекцию в виде прямой на П1. Прямая общего положения — прямая, не параллельная и не перпендикулярная ни одной из плоскостей проекций. Прямая уровня прямая, параллельная одной из плоскостей проекций. Фронталь параллельна плоскости П2.

Экватор это наибольшая параллель. Список рекомендуемой литературы 1. Чекмарев, А.А. Инженерная графика: учебник для немаш.

Краткий курс начертательной геометрии / О.В. Начертательная геометрия. Инженерная и машинная графика / А.А. Образец заявления на продленку. Чекмарев и др. Инженерная графика: учебник / А.И. Начертательная геометрия / Н.Н.

Крылов и др. М., 2003. Начертательная геометрия: учебник для вузов / Н.Н. Крылов и др.; под ред. 7-е изд., перераб. Список используемых источников 1. Подоплелов, Е.В.

Методические указания и контрольные задания по инженерной графике / Е.В. Подоплелов, Н.А. Устюгова, Н.В. – Ангарск: АГТА, 2008 50. Начертательная геометрия: конспект лекций / А.А.

Ляшков, Л.К.Куликов, К.Л. – Омск: Изд-во ОмГТУ, 2005. Хрусталева, Т.В.

Начертательная геометрия: учебное пособие / Т.В. Хабаровск: Изд-во ДВГУПС, 2003. Задания на контрольную работу № 1: методические указания и контрольные вопросы по курсу «Начертательная геометрия» / Е.В. Грачев и др. СПб.: Санкт-Петербургский университет ГПС МЧС России, 2008.

Лексаченко, Т.А. Начертательная геометрия: методические указания по решению задач с условиями задач / Т.А. СПб.: Санкт-Петербург, 2005. Материал взят из книги Инженерная графика (О.А.

Располагайте инструкцию рядом с пультом. Пульт управления ВКЛ / ВЫКЛ. Прибор для повторного включения двухконтурного котла Navien. Котел навьен делюкс инструкция пульт управления.

Предмет начертательной геометрии Начертательная геометрия – одна из фундаментальных дисциплин инженерного образования, где пространственные фигуры изучаются по их проекционным изображениям. Основной целью данной дисциплины является разработка методов изображения геометрических фигур на плоскости или на другой поверхности и дальнейшее их применение при решении задач. Методы начертательной геометрии позволяют с высокой степенью точности решать математические задачи графически. В изобразительном искусстве, архитектуре и строительстве метод проекций позволяет получать наглядные изображения создаваемых объектов. Задачи начертательной геометрии решаются графическим путем.

Знание базовых правил и теорем позволяет решать сложные задания путем расчленения процесса их решения на ряд элементарных однотипных операций. Основополагающей операцией, которую приходится выполнять в процессе решения, является определение точки пересечения двух линий. Начертательная геометрия является одним из лучших средств развития у человека пространственного воображения, логического мышления, без которых сложно представить любое инженерное творчество. Основные виды задач называются задачи, в которых требуется определить действительные значения величин плоских фигур, углов, отрезков, расстояний или построить геометрические объекты заданных размеров. В общем случае геометрические фигуры произвольно расположены по отношению к плоскостям проекций и проецируются на эти плоскости с искажением их линейных и угловых величин.

Чтобы определить натуральную величину любой плоской фигуры, ее нужно перевести в положение, при котором она будет параллельна одной из плоскостей проекций. Называются задачи, в которых требуется определить взаимное положение геометрических объектов – построить линию их пересечения или определить принадлежность точки некоторой фигуре. Для решения позиционных задач обычно используют ряд вспомогательных поверхностей. Их выбирают таким образом, чтобы они пересекались с заданными фигурами по линиям, которые просты для построения – например, по прямым и окружностям. В начертательной геометрии существуют базовые задачи, без освоения которых невозможно дальнейшее изучение предмета. Это построение ортогональных проекций точек и поверхностей, определение следов прямых и плоскостей. Владение проекций позволяет самостоятельно анализировать и значительно упрощать решение многих задач.

Начертательная Геометрия 1 Курс

Решение задач по алгоритму.